
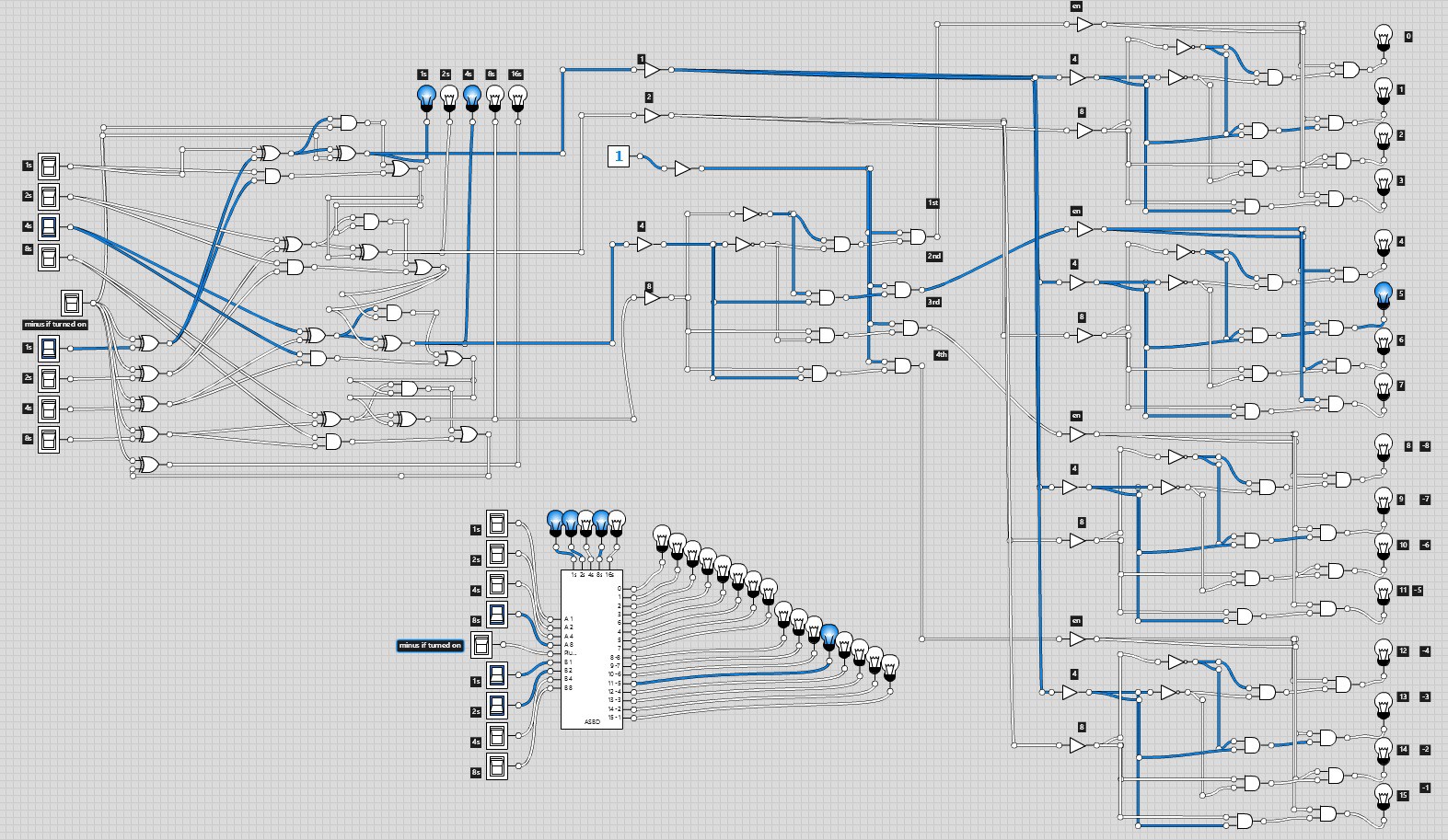

Similarly in an unsigned operation carry flag is monitored and overflow flag is ignored. In a signed operation overflow flag is monitored and carry flag is ignored.
Overflow vs Carry: Overflow can be considered as a two's complement form of a Carry. Conveniently, an XOR operation on these two bits can quickly determine if an overflow condition exists. In a signed operation if the two leftmost carry bits (the ones on the far left of the top row in these examples) are both 1s or both 0s, the result is valid if the left two carry bits are "1 0" or "0 1", a sign overflow has occurred.
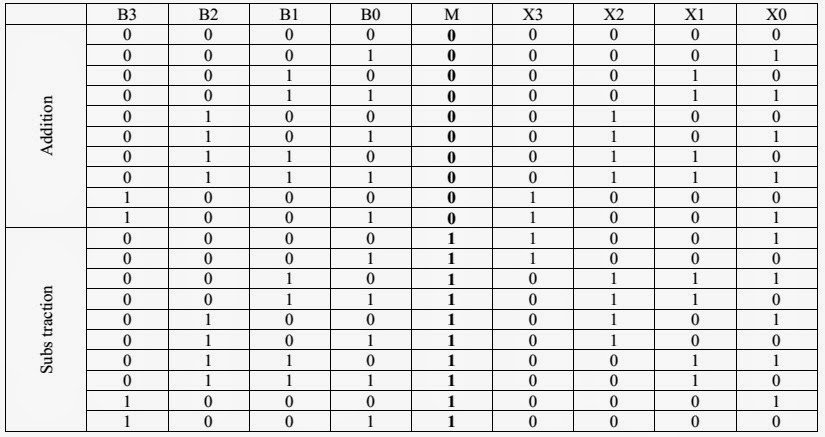
If the sum of two negative numbers yields a positive result, the sum has overflowed. If the sum of two positive numbers yields a negative result, the sum has overflowed. An overflow results in invalid operation. Negative numbers are represented in 2's complement. MSB is always reserved to indicate sign of the number. Some points to remember in a signed operation: Otherwise, if it is '0', the subtracted number should be negative, wich an unsigned number can not represent.Overflow flag indicates an overflow condition for a signed operation. So the last carry-bit by an unsigned subtraction has to be set to '1' if the calculation was performed right. 1111Īnd there, as you can see is the (right) overflow. We rember: 2's complement = invert the number and add 1Īnd then we add this number on our 15. So what do we add on "1111" to get "0000"? Simply just a "0001", which ist the Two's complement of 15. The fact, that we can't represent all positive numbers is the solution (with 4 bit is the unsigned maximum 15).įor example we calculate 15 - 15 with 4 bit unsigned numbers. The only way, to decrease an unsigned number with only an adder, is to overflow it. I dont have any subtractor and i can't represent a negatie number. So in fact, i simply can't calculate 4 - 1. With unsigned numers i can't represent a negative number. However in signed addition, we can calculate for exampe 4 + (-1). The ripple carry adder consists of more (here 4) full adders. Ok, i slept and now evrything is much clearer -)Īfter an unsigned subtraction the carry has to be '1' otherwise there is an overflow, an here is why. So it tells me that 14-15 is 15 (which is not surprising) but the overflow flag is set to 0.ĭid i misunderstood the subtraction overflow bit, or is a unsigned_cout xor sub missing? So to understand my troubles with the unsigned carry let's calculate 1111 - 1111 in unsigned. In my opinion i have build it the right way. Here is on page 11 the circuit which i have build. It works fine, except for one thing.Ĭarry after an unsigned subtraction doesn't behave, how i expected. I have almost successfully implemented n-bit adder-subtractor.







 0 kommentar(er)
0 kommentar(er)
